Журнал «Травма» Том 16, №2, 2015
Вернуться к номеру
Математическое моделирование контактных напряжений и объема движений в локтевом суставе при переломе блока плечевой кости со смещением
Авторы: Макаров В.Б. — ГУ «Специализированная медико-санитарная часть № 6», г. Днепропетровск; Левадный Е.В. — Днепропетровский национальный университет; Страфун А.С. — Отдел микрохирургии и реконструктивно-восстановительной хирургии верхней конечности НИИ травматологии и ортопедии НАМН Украины, г. Киев
Рубрики: Травматология и ортопедия
Разделы: Клинические исследования
Версия для печати
Авторами построена необходимая геометрическая модель локтевого сустава, соответствующая требованиям к проведению математического моделирования. В программной среде ABAQUS на основе построенной геометрической модели был смоделирован перелом 13B2 (AO/ASIF) дистального отдела плечевой кости с различными величинами смещения суставной поверхности блока плечевой кости — 2, 3, 4 и 5 мм. На основе геометрической модели создана расчетная конечно-элементная модель и выполнен численный эксперимент. Установлено, что с ростом величины смещения отломка плечевой кости растет величина контактного напряжения суставных поверхностей в плечелучевом суставе с одновременным уменьшением площади контакта. Контактные напряжения суставных поверхностей резко возрастают при смещении фрагментов на 4–5 мм. Установлена зависимость угла сгибания и величины смещения отломка в зависимости от роста контактных напряжений, которая показывает, что смещение отломка на 2–3 мм в случае перелома 13В2 (AO/ASIF) существенно не уменьшает угол сгибания в локтевом суставе, несмотря на повышение контактных напряжений до 20–30 % по сравнению с физиологическими напряжениями. Данный факт может свидетельствовать о возможности консервативного лечения и последующей активной реабилитации. Таким образом, смещение внутрисуставных отломков на 2–3 мм можно рассматривать как максимально допустимое смещение, которое не будет в значительной степени ограничивать движения в локтевом суставе.
Авторами побудована необхідна геометрична модель ліктьового суглоба, що відповідає вимогам до проведення математичного моделювання. У програмному середовищі ABAQUS на основі побудованої геометричної моделі був змодельований перелом 13B2 (AO/ASIF) дистального відділу плечової кістки з різними величинами зміщення суглобової поверхні блоку плечової кістки — 2, 3, 4 і 5 мм. На основі геометричної моделі створена розрахункова кінцево-елементна модель та виконано чисельний експеримент. Встановлено, що зі збільшенням величини зміщення уламка плечової кістки збільшується величина контактного напруження суглобових поверхонь в плечепроменевому суглобі з одночасним зменшенням площі контакту. Контактні напруження суглобових поверхонь різко зростають при зміщенні фрагментів на 4–5 мм. Встановлено залежність кута згинання і величини зміщення уламка залежно від зростання контактних напружень, яка показує, що зміщення уламка на 2–3 мм в разі перелому 13В2 (AO/ASIF) істотно не зменшує кут згинання в ліктьовому суглобі, незважаючи на підвищення контактних напружень до 20–30 % у порівнянні з фізіологічними напруженнями. Даний факт може свідчити про можливість консервативного лікування і подальшої активної реабілітації. Отже, змiщення внутрішньосуглобових уламків на 2–3 мм можна розглядати як максимально допустиме зміщення, що не буде значною мірою обмежувати рухи в ліктьовому суглобі.
The authors constructed a necessary geometrical model of the elbow joint that meets sufficient requirements for mathematical modeling. In ABAQUS software, based on created geometric model, there has been simulated 13B2 (AO/ASIF) fracture of the distal humerus with different values of displacement of the articular surface of the humeral trochlea — 2, 3, 4 and 5 mm. On the basis of geometrical model, finite element model has been created and numerical experiment has been carried out. It was found that with increase in the displacement of the fragment of the humerus, the value of contact stress in the articular surfaces in the humeroradial joint increases with simultaneous reduction of the contact area. Contact stress on joint surfaces rise sharply at 4–5 mm displacement of fragments. There has been shown a dependence of the angle of flexion and the value of displacement of fragments on the growth of contact stresses, which shows that the amount of displacement of fragment by 2–3 mm in case of 13B2 fracture (AO/ASIF) did not significantly reduce the elbow angle, despite an increase in contact stresses up to 20–30 % compared with the physiological stresses. This fact may indirectly indicate a possibility of conservative treatment and further active rehabilitation. Thus, displacement of intraarticular fragments by 2–3 mm can be considered as maximal allowable displacement that will not greatly restrict the movements of the elbow joint.
перелом дистального отдела плеча, объем движений, площадь контактных напряжений, напряженно-деформированное состояние, конечно-элементная сетка.
перелом дистального відділу плеча, обсяг рухів, площа контактних напружень, напружено-деформований стан, кінцево-елементна сітка.
distal humerus fracture, range of motion, contact stress area, stress-strain state, finite-element mesh.
Статья опубликована на с. 9-19
Введение
Лечение внутрисуставных переломов дистального отдела плечевой кости — сложная и многогранная проблема. Переломы данной локализации являются сравнительно редкой травмой в структуре повреждений опорно-двигательной системы и составляют до 2 % от всех переломов [1]. При этих повреждениях чрезвычайно трудно достичь максимально возможного функционального результата. Спорными остаются вопросы показаний и противопоказаний к консервативному лечению, особенностей хирургического доступа, методов фиксации при открытой репозиции [2, 3]. Особую проблему данный вид повреждения представляет у пациентов старше 60 лет. Длительная иммобилизация у таких пациентов (более 14 суток) вызывает резкое ухудшение функции локтевого сустава и снижение потенциала для восстановления движений в минимально необходимом физиологическом объеме по Morrey 100° [4]. В связи с этим остается нерешенным вопрос, при каком минимальном смещении отломков, составляющих суставную поверхность, можно получить достаточную функцию локтевого сустава при активной реабилитации. Для ответа на данный вопрос необходимо изучить контактные взаимодействия между суставными поверхностями при моделировании внутрисуставного перелома дистального метаэпифиза плечевой кости. Ряд авторов исследовали контактные напряжения на трупном материале [5–7]. Несмотря на максимальную объективность физического эксперимента, весьма трудно учесть разницу между минеральной плотностью разных препаратов, а также невозможность повторения опыта на одном и том же материале из-за стрессовых перегрузок и его полного или частичного разрушения. Математическое моделирование, или численный эксперимент, лишено этих недостатков [8].
Цель исследования — с помощью математического моделирования определить зависимость между контактными напряжениями, а также площадью контакта в плечелучевом и плечелоктевом суставах и возможной амплитудой движений в локтевом суставе при внутрисуставном переломе дистального отдела плечевой кости с различной величиной смещения — 2, 3, 4 и 5 мм.
Материалы и методы
На основе данных, предоставленных компанией Zygote Media Group, Inc., U.S. (http://www.3dscience.com), построена необходимая геометрическая модель (рис. 1), отвечающая требованиям к проведению математического моделирования.
/13/13.jpg)
Для последующего анализа был выбран тип перелома 13B2 (AO/ASIF) дистального отдела плечевой кости. Переломы типа B дистального метаэпифиза плечевой кости возникают при падении на кисть с разогнутым локтевым суставом, в сочетании с абдукцией предплечья. При этом нередко ломается и локтевой отросток. Перелом типа В2 может быть результатом прямого удара в область локтевого сустава, а именно медиального надмыщелка.
Этот тип перелома является внутрисуставным, что, безусловно, влияет на функциональный исход, и достаточно простым для моделирования смещения относительно суставной поверхности блока плечевой кости величиной 2, 3, 4 и 5 мм (рис. 2).
В программной среде ABAQUS на основе построенной геометрической модели для проведения математического моделирования (численного анализа) создана расчетная модель в виде конечно-элементной сетки, отражающей геометрию и физические характеристики тел; контактные элементы, позволяющие средствами нелинейного расчета отразить динамическое взаимодействие различных тел между собой; нагрузки и закрепления, уточняющие физическую картину работы расчетной модели и позволяющие определить объем движения в локтевом суставе при различных величинах смещения блока плечевой кости. Также конечно-элементная модель использовалась для прогноза площади контакта суставных поверхностей при различных смещениях отломков. Конечно-элементная сетка (рис. 3, 4) расчетной модели состоит из 396 607 элементов, 390 353 из которых являются C3D4 (4-узловой элемент, линейный тетраэдр).
Так как анализ данной задачи подразумевает расчет модели при различных углах поворота костей в локтевом суставе, то, чтобы учесть взаимное влияние разных тел, входящих в модель, задача ставилась как контактная, с учетом возможности возникновения контакта между отдельными участками контактирующих тел. Влияние связок и капсулы локтевого сустава в данном расчете не учитывалось.
Нагрузки и закрепления. Мы допустили, что положение локтевой и плечевой костей при пронации-супинации остается неизменным. Чтобы сохранить обратное влияние на лучевую и локтевую кость со стороны контактирующих участков зафиксированных костей, фиксация была выполнена в узлах конечно-элементной сетки, наиболее удаленных от мест контакта. Так как предполагается анализ результатов расчетов статических задач уравновешенных моделей при различных углах сгибания в локтевом суставе, то каждый расчет подразумевает наличие уравновешивающей системы сил, действующих на модель. Нагружение лучевой и локтевой костей предполагает получение уравновешенного состояния за счет осевого давления на диафизарную часть с одной стороны и реакции опоры со стороны головки и блока плечевой кости.
Таким образом, задавая осевую нагрузку на лучевую и локтевую кость в направлении локтевого сустава, зафиксировав при этом положение плечевой кости, мы получим установившееся статическое положение системы.
Для оценки осевой нагрузки на лучевую и локтевую кость примем, что эта нагрузка появляется вследствие отжимания на руках. Отметим, что лучевая кость принимает 70–80 % нагрузки [9]. Предположим, что вес человека составляет 100 кг:
G = 100 (кг),
т.е. сила притяжения будет составлять:
F веса = G • 9,81 = 100 • 9,81 = 981 (Н).
С учетом того, что при отжимании человек перераспределяет нагрузку от силы тяжести на 4 конечности, сила реакции опоры на одну руку будет составлять:
R = 981 : 4 = 245,25 (Н).
Так как предплечье состоит из 2 костей, то сила, действующая вдоль одной лучевой и локтевой кости, будет составлять:
R лучевой = 245,25 • 0,7 = 171,67 (Н);
R локтевой = 245,25 • 0,3 = 73,57 (Н).
Следует заметить, что если величина осевой нагрузки на лучевую и локтевую кость приведет к достаточно большим напряжениям, то на практике это вызовет ее разрушение. Результаты расчета не смогут показать разрушение как таковое. Но причины, приводящие к дальнейшему разрушению, могут быть обнаружены. Поэтому после получения результатов расчетов и до начала анализа следует оценить уровень напряжений по отношению к максимально допустимым значениям, которые приведены в соответствующих свойствах материалов.
В расчетную модель входит три суставных поверхности плечевой, лучевой и локтевой костей. Кроме того, контактные участки моделировались с учетом снижения уровня модуля Юнга, отражая особенности наличия хрящевой ткани на контактных поверхностях костей. Расчет включал в себя анализ напряженно-деформированного состояния системы при углах сгибания в локтевом суставе 30, 60, 90 и 120° и в среднем положении между пронацией и супинацией.
Свойства материалов, а также характер нагружения модели для всех расчетов были приняты постоянными и одинаковыми (табл. 1, 2) [10, 11]. Величина коэффициента Пуассона для всех материалов была принята равной 0,3.
Результаты и их обсуждение
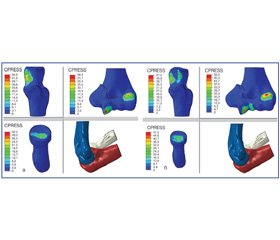
В результате расчета были получены контактные напряжения на суставных поверхностях локтевого сустава в норме, а также различные площади контакта суставных поверхностей и величины контактных напряжений в зависимости от угла возможного сгибания локтевого сустава при внутрисуставном переломе дистального метаэпифиза плеча типа 13В2 (рис. 5).
Анализ контактных площадей. Установлено, что площадь контакта между локтевой и плечевой костями в случае смещения отломков на 2 мм по линии перелома больше на 30 %, чем при смещении на 5 мм и угле сгибания 90° (рис. 5).
Анализируя данные табл. 3, следует отметить, что при переломе блока плечевой кости со смещением от 2 до 5 мм площадь контакта головки лучевой кости с головкой мыщелка плечевой кости изменяется незначительно в зависимости от угла сгибания (рис. 6), при этом чем больше угол сгибания, тем больше площадь контакта. При рассмотрении площади контакта блока плечевой кости с локтевым отростком увеличение смещения отломков приводит к уменьшению площади контакта, а увеличение угла сгибания уменьшает величину площади контакта (рис. 7).
/15/15_2.jpg)
Данные о величинах контактных напряжений на головке лучевой кости, локтевом отростке и плечевой кости при различных углах сгибания в локтевом суставе и различной величине смещения представлены на графиках (рис. 8–10).
Анализ данных контактных напряжений. Приняв среднефизиологическое контактное напряжение на суставных поверхностях в норме 5,5–8,5 МПа [12, 13], установили, что до угла сгибания 90° напряжение медленно растет. В среднем при смещении отломков на 2–3 мм и до угла сгибания до 90° рост контактных напряжений составляет 20–30 %. При угле сгибания 90° в локтевом суставе напряжения на суставной поверхности лучевой кости возрастают с 23 МПа при смещении отломков на 2 мм до 26 МПа, а при смещении на 5 мм на локтевом отростке с 21 до 32 МПа, на плече — с 23 до 32 МПа (рис. 11). При угле сгибания 120° контактные напряжения возрастают с 33–37 до 45–50 МПа.
/17/17.jpg)
Таким образом, исходя из вышепредставленных данных, а именно из уменьшения площади контакта суставных поверхностей локтевой и плечевой костей при увеличении смещения отломков и угла сгибания в локтевом суставе, а также увеличения контактных напряжений на суставных поверхностях, можно предположить, что ограничение угла сгибания происходит как из-за нарушения конгруэнтности суставных поверхностей, так и из-за нарастания болевого синдрома, вызванного повышением давления на суставных поверхностях.
Приняв контактное напряжение на суставных поверхностях, при котором начинается резкий рост контактных напряжений (в среднем 24 МПа), за начальное условие для построения зависимости угла сгибания и величины смещения отломка в зависимости от роста контактных напряжений, можно построить график (рис. 12).
/18/18.jpg)
Из графика на рис. 12 видно, что смещение отломка в случае перелома В2 (AO/ASIF) на 2–3 мм значительно не уменьшает угол сгибания в локтевом суставе, что может косвенно свидетельствовать о возможности консервативного лечения (иммобилизации не более 14 суток) и последующей активной реабилитации.
Выводы
1. С помощью разработанной трехмерной конечно-элементной модели локтевого сустава возможно выполнять исследование напряженно-деформированного состояния как в норме, так и при моделировании перелома.
2. При рассмотрении площади контакта блока плечевой кости с локтевым отростком увеличение смещения отломков приводит к уменьшению площади контакта, а увеличение угла сгибания уменьшает площадь контакта.
3. Установлено, что площадь контакта между локтевой и плечевой костями в случае смещения отломков на 2 мм по линии перелома больше на 30 %, чем при смещении на 5 мм и угле сгибания 90°.
4. Из-за уменьшения площади контакта суставных поверхностей локтевой и плечевой костей при увеличении смещения отломков и угла сгибания в локтевом суставе, а также увеличении контактных напряжений на суставных поверхностях можно предположить, что ограничение угла сгибания происходит как из-за нарушения конгруэнтности суставных поверхностей, так и из-за нарастания болевого синдрома, вызванного повышением давления на суставных поверхностях.
5. Установлено, что с ростом величины смещения отломка плечевой кости увеличивается контактное напряжение суставных поверхностей в плечелучевом суставе с одновременным уменьшением площади контакта. Контактные напряжения суставных поверхностей резко возрастают при смещении фрагментов на 4–5 мм (до 45–50 МПа).
6. Установлена зависимость угла сгибания и величины смещения отломка от роста контактных напряжений, которая показывает, что смещение отломка на 2–3 мм в случае перелома 13В2 (AO/ASIF) значительно не уменьшает угол сгибания в локтевом суставе, несмотря на повышение контактных напряжений до 20–30 % в сравнении с физиологическими напряжениями. Данный факт может косвенно свидетельствовать о возможности консервативного лечения и последующей активной реабилитации. Таким образом, смещение внутрисуставных отломков на 2–3 мм можно рассматривать как максимально допустимое смещение, которое не будет в значительной мере ограничивать движения в локтевом суставе.
1. Garcia J.A., Mykula R., Stanley D. Complex fractures of the distal humerus in the elderly // J. Bone Joint Surg [Br]. — 2002. — 84-B. — 812-6.
2. Wang Y., Zhuo Q, Tang P, Yang W. Surgical interventions for treating distal humeral fractures in adults // Cochrane Database Syst. Rev. — 2013 Jan 31.
3. Korner J., Lill H., Müller L.P., Hessmann M., Kopf K., Goldhahn J., Gonschorek O., Josten C., Rommens P.M. Distal humerus fractures in elderly patients: results after open reduction and internal fixation // Osteoporos Int. — 2005 Mar. — 16, Suppl. 2. — S73-9. Epub 2004 Oct 29.
4. Morrey B. The elbow and its disorders / B. Morrey. — 3ed. — Philadelphia; London; New York: W.B. Saunders company, 2000. — 934 p.
5. Shepard M.F., Markolf K.L., Dunbar A.M. Effects of radial head excision and distal radial shortening on load-sharing in cadaver forearms // J. Bone Joint Surg. Am. — 2001 Jan. — 83-A(1). — 92-100.
6. Rao Z.T., Yuan F., Li B., Ma N. Effect of elbow flexion angles on stress distribution of the proximal ulnar and radius bones under a vertical load: measurement using resistance strain gauges // J. Orthop. Surg Res. — 2014 Jul. — 31, 9. — 60.
7. Eckstein F., Löhe F., Hillebrand S., Bergmann M., Schulte E., Milz S., Putz R. Morphomechanics of the humero-ulnar joint: I. Joint space width and contact areas as a function of load and flexion angle // Anat. Rec. — 1995 Nov. — 243 (3). — 318-26.
8. Edmonds E.W., Santago A.C. 2nd, Saul K.R. Functional Loss With Displacement of Medial Epicondyle Humerus Fractures: A Computer Simulation Study // J. Pediatr. Orthop. — 2014 Dec 9.
9. Pfaeffle H.J., Fischer K.J., Manson T.T., Tomaino M.M., Woo S.L., Herndon J.H. Role of the forearm interosseous ligament: is it more than just longitudinal load transfer? // J. Hand Surg. Am. — 2000. — 25. — 683-688.
10. Карлов А.В. Системы внешней фиксации и регуляторные механизмы оптимальной биомеханики / А.В. Карлов, В.П. Шахов. — Томск: STT, 2001. — 480 с.
11. Трушко А.В. АСМ-анализ хрящевых тканей / А.В. Трушко, С.А. Чижик: Мат-лы VII Междунар. семинара (1–3 ноября 2006 г., Минск). — Минск: ИТМО НАН Беларуси, 2006. — С. 162-168.
12. Бойко И.В. Биомеханическое изучение особенностей распределения нагрузок в головке и шейке лучевой кости / И.В. Бойко, В.Б. Макаров, Д.Е. Щербаков и др. // Вісник ортопедії, травматології та протезування. — 2013. — № 1. — С. 22-27.
13. Kim. Sunghwan Contact Stress Analysis of the Native Radial Head and Radial Head Implants: Doctoral Dissertation. — University of Pittsburgh, 2014. —119 p.

/13/13_2.jpg)
/14/14.jpg)
/15/15.jpg)
/16/16.jpg)
/17/17_2.jpg)